【学习笔记】CS229机器学习--回归方法
-
线性回归
线性回归假设特征和结果满足线性关系。其实线性关系的表达能力非常强大,每个特征
对结果的影响强弱可以有前面的参数体现,而且每个特征变量可以首先映射到一个函数,然
后再参与线性计算。这样就可以表达特征与结果之间的非线性关系。太简单了不写公式了
梯度下降法
梯度下降法是按下面的流程进行的:
1)首先对 θ 赋值,这个值可以是随机的,也可以让 θ 是一个全零的向量。
2)改变 θ 的值,使得 J(θ)按梯度下降的方向进行减少。
梯度方向由 J(θ)对 θ 的偏导数确定,由于求的是极小值,因此梯度方向是偏导数的反方向。
结果为
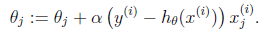
迭代更新的方式有两种,一种是批梯度下降,也就是对全部的训练数据求得误差后再对 θ
进行更新,另外一种是增量梯度下降,每扫描一步都要对 θ 进行更新。前一种方法能够不断
收敛,后一种方法结果可能不断在收敛处徘徊。最小二乘法
将训练特征表示为 X 矩阵,结果表示成 y 向量,仍然是线性回归模型,误差函数不变。那么
θ 可以直接由下面公式得出
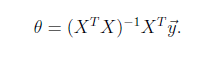
但此方法要求 X 是列满秩的,而且求矩阵的逆比较慢。
用误差函数为平方和的概率解释
假设根据特征的预测结果与实际结果有误差,那么预测结果和真实结果满足下
式:
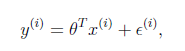
一般来讲,误差满足平均值为 0 的高斯分布,也就是正态分布。那么 x 和 y 的条件概率也就
是
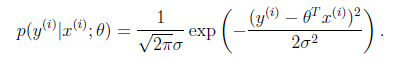
牛顿法来解最大似然估计
当要求解f(θ) = 0时,如果 f 可导,那么可以通过迭代公式
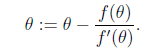
来迭代求解最小值。
当应用于求解最大似然估计的最大值时,变成求解ℓ ′ (𝜃) = 0的问题。
那么迭代公式写作
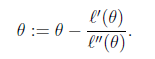
当 θ 是向量时,牛顿法可以使用下面式子表示

其中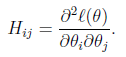
H是n*n的 Hessian 矩阵。一般线性模型
首先,如果一个概率分布可以表示成
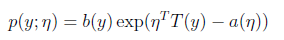
那么这个概率分布可以称作是指数分布。在对数回归时采用的是伯努利分布,伯努利分布的概率可以表示成

其中
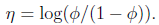
得到
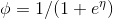
所以对数回归要用这个函数
Softmax 回归
假设预测值 y 有 k 种可能,即 y∈{1,2,…,k}
定义
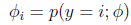
有
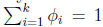
所以有
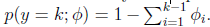
即式子左边可以有其他的概率表示,因此可以当做是 k-1 维的问题。
我们假设T(y)这时候是一组 k-1 维的向量,不再是 y。即 T(y)要给出 y=i(i 从 1 到 k-1)的概率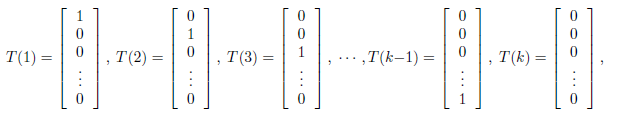
应用于一般线性模型
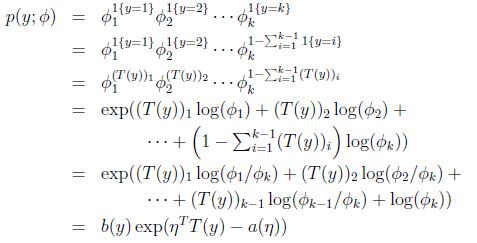
那么
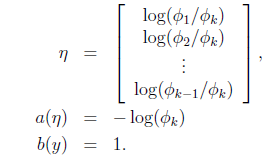
最后求得

而 y=i 时的概率改写为
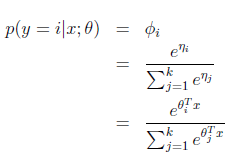
那么整体期望值

最后就获得了最大似然估计